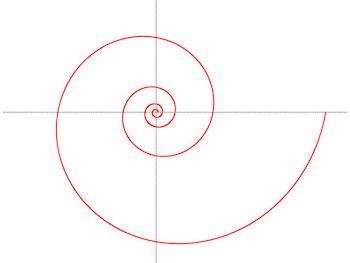
logarithmic spiral definition
The logarithmic spiral is a spiral frequently sighted in nature and that was analyzed first by Descartes. Later, another man named Jacob Bernoulii researched the spiral, and dubbed it the “Spira mirabilis” - the marvelous spiral. Jacob was so taken with the spiral he wanted it engraved on his tombstone. One of the reasons he was so interested by the spiral was because of its unusual mathematical property of retaining its shape despite the size of the spiral increasing.
The spiral is related to the golden ratio, the Fibonacci numbers and the golden rectangles. The spiral can be created by spacing rays equally at a point along a ray and placing a perpendicular line to the nearby ray. The more the rays increase, the smooth the logarithmic spiral becomes. It is also called the equiangular spiral and the growth spiral. It is different than another type of spiral called the Archimedean spiral because the revolving of a logarithmic spiral grows in geometric progression, whereas in an Archimedean spiral those same distances remain the same.
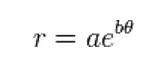
The logarithmic curve can be written in polar coordinates as this equation.